The Gamma of an option measures the rate of change of the option delta. Its' number is denoted relative to a one point move in the underlying asset. For example, if the gamma for an option shows 0.015 with a delta of 0.45 then a full point move in the stock (i.e. 35 to 36) means the delta will move to 0.465.
Gamma is calculated via an option model such as Black and Scholes or Binomial. The value is the same for both call and put options.
The Gamma of an option is important to know because the delta of an option is not constant; the delta increases and decreases as the underlying moves. Because delta is essentially our position value in the underlying, the gamma therefore tells traders how fast their position will increase or decrease in value vs movements in the underlying asset.
In other words, Gamma shows how volatile an option is relative to movements in the underlying asset. So, watching your gamma will let you know how large your delta (position risk) changes.
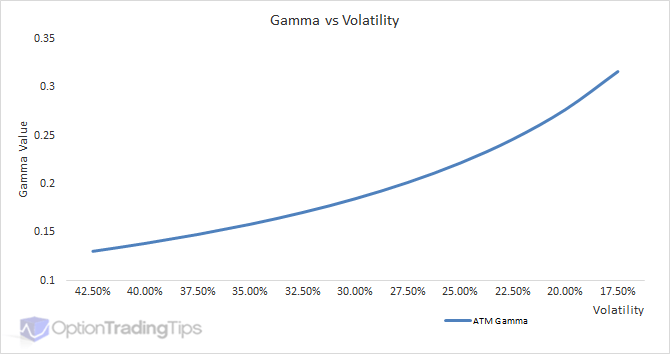
Gamma is not linear. Like Delta, Gamma has curvature and is effected by the inputs that calculate the Gamma, the most notable forces that influence it are factors such as the difference between the strike price and the underlying price, the time to expiration of the option and the implied volatility used in the model. Interest rates and dividends are also factors that effect the value of the Gamma, however, the magnitude of these inputs is minimal when compared to the previously mentioned variables.
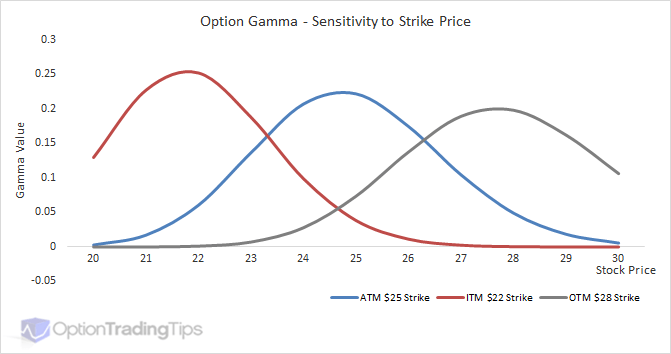
The attention on a Gamma's sensitivity is mostly focused on its' position relative to the underlying price. Looking at the above graph you can see that the Gamma reaches its' peak when the option is at-the-money and tapers off either side. When an option position moves towards the ATM level, the changes in the position delta, and hence the position value relative to the stock, change with greater amounts. Options that are either deep ITM or deep OTM experience less variability as the stock price changes and therefore will show low Gamma values.
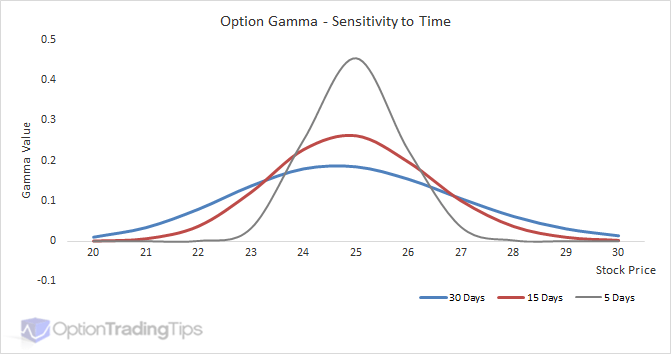
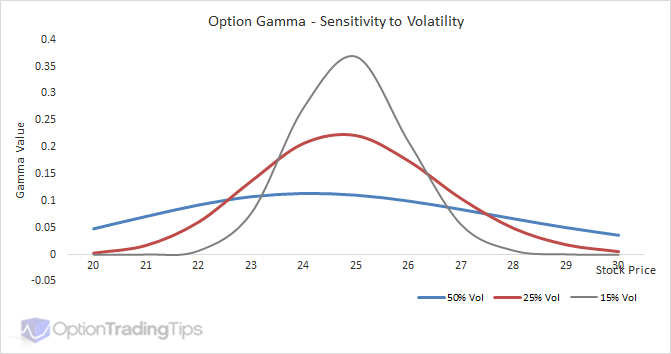
Adding more time to an option contract increases the likelihood of that option expiring in-the-money. Because higher volatility also increases the chances of an option's in-the-moneyness, both volatility and time have the same effect on an option's Gamma value.
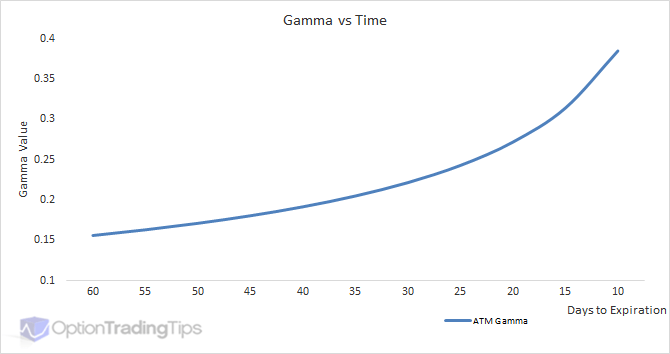
The above graphs show how increasing time/volatility value reduces the Gamma of the option and hence it's sensitivity to changes in stock price.
While adding more time to an option increases the VAUE of the option, it generally reduces the option's Gamma. With more time to expiration the option becomes less sensitive to movements in the underlying asset. However, as the option approaches its' maturity date, its' time value will move towards zero and then become more responsive to changes in the underlying price.
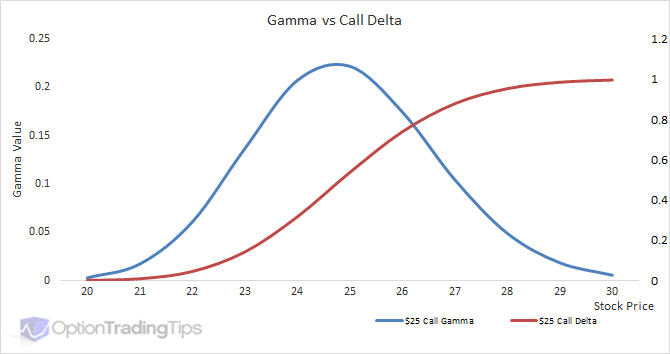
These graphs provide a great way to look at how Gamma is effected by the passage of time. Both plot a $25 call option's Gamma across a range of underlying prices, however, on each graph is shown 3 different times to maturity. This is so you can see how the Gamma value becomes the highest when it is both ATM and close to expiration. When this happens, option positions will have the highest fluctuations in position value (Delta).
Note: The Gamma value is the same for calls as for puts. If you are long a call or a put, the gamma will be a positive number. If you are short a call or a put, the gamma will be a negative number.
When you are "long gamma", your position will become "longer" as the price of the underlying asset increases and "shorter" as the underlying price decreases.
Conversely, if you sell options, and are therefore "short gamma", your position will become shorter as the underlying price increases and longer as the underlying decreases.
This is an important distinction to make between being long or short options - both calls and puts. That is, when you are long an option (long gamma) you want the market to move. As the underlying price increases, you become longer, which reinforces your newly long position.
If being "long gamma" means you want movements in the underlying asset, then being "short gamma" means that you do not want the price of the underlying asset to move.
A short gamma position will become shorter as the price of the underlying asset increases. As the market rallies, you are effectively selling more and more of the underlying asset as the delta becomes more negative.
The graphs shown here, display gamma with constant volatility and strike price. In practice, options across different strike prices have different implied volatilities and therefore a different gamma distribution.
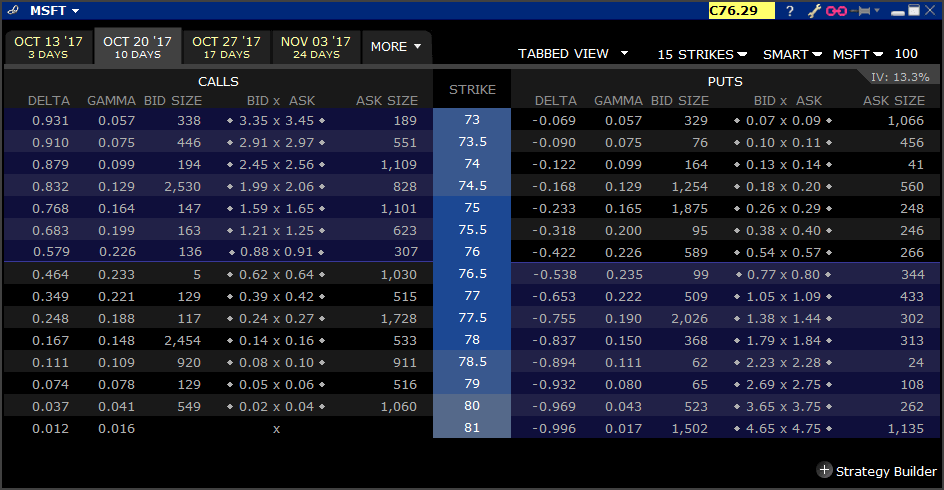
The above is an example of what Gamma and Delta values look in practice. This is an option chain of MSFT stock options showing an expiration 10 days out.
Notice how the ATM strike of $76.50 shows the highest Gamma value of 0.233 for the calls and 0.235 for the puts. I'm not sure why they are different here...they really should show exactly the same value for the call and the put - perhaps a rounding issue. Nevertheless, 0.002 difference is fairly immaterial.
If the stock trades up 1 full point to $77.29 then the $76.50 call option Delta will move from 0.464 to 0.697. So while the stock price has only moved 1.3% your effective position in the underlying has increased by 50%.
If you're interested in knowing how to calculate option gamma in excel, you can download my option pricing spreadsheet for a working example. Otherwise, here are some code examples:
Option Gamma Formula
Where:
ArwenJuly 17th, 2014 at 1:30am
Thanks again,Peter!
Your explanation is very clear :-)
PeterJuly 17th, 2014 at 12:52am
Hi Arwen,
When your position is "long gamma" it means that upward movements in the underlying price increase your delta (longer). Conversely, downward movements in the base price reduce your position delta (shorter).
In the above, as the market rallies and your position becomes longer in delta you must sell the underlying to remain delta neutral. As the market begins to sell off, you then become shorter requiring you to buy back deltas.
So, as the market rallies, you're selling into it - when it falls you're buying it back. If this is done in large quantities it can have the effect of restricting the movement of the stock.
The reverse is true for short gamma; as the market rallies, your position delta becomes shorter and you'll need to hedge by buying stock. In this case you're buying as the market rallies to square up your delta and selling as the market falls.
Does that explanation help?
ArwenJuly 16th, 2014 at 2:38am
Hello Peter,
I have a question on relationship between "keeping delta-neutral position" and "volatility movements".
If the market participant wants to keep delta-neutral position (net positive gamma) by the action of buying and selling large number of stock, then this dampens volatility.
If the market participant wants to keep delta-neutral position (net negative gamma) by the action of buying and selling large number of stock, then this increases volatility.
I am not very clear about the relationship behind them. Could you please give some explanation? Thank you very much!!
ArwenJuly 13th, 2014 at 2:28am
Thanks, Peter!
Now, I understand that, from a seller's point of view, the short position is worthless.
PeterJuly 12th, 2014 at 4:45am
Hi Arwen,
When you buy an option you pay the premium (option price) to the option seller; so as the option seller you receive the premium at the time of trade.
With a short position, you want the price of the option to decrease, ideally to zero, at which point the option will be worthless. Once the option expires worthless, you, the option seller have benefited by retaining the premium received by the buyer of the option.
If the price of the option increases, you may end up buying the option back (to square of your short position) at a higher price than what you sold it for, which means you will make a loss in this situation.
Let me know if anything is still unclear.
ArwenJuly 12th, 2014 at 2:16am
Hi Peter,
You answered Darryl's question on 4.30.2012.
You said "If you are short the position is still worthless, however, you make a profit - being the premium received for selling the option." I am confused. If the position is short, we can make profit. But why the position is still worthless? How to explain this?
Thank you!!
PeterApril 23rd, 2014 at 6:56am
Hi Rawdy,
Short gamma volatility trades typically want volatility and market movements to remain stable so if the market gaps large and you are short gamma and delta neutral you will lose money.
However, you can be short gamma and also short delta i.e. short naked call option. In this case if the market gaps open lower you will most likely be making money in this situation.
rawdyApril 20th, 2014 at 3:27am
what if gamma is short and market open gap down will i make loss or profit
PeterApril 30th, 2012 at 7:25pm
Hi Darryl,
The Position Delta = Delta x Contract Size x Number of Option Contracts.
In the post by Charlie, he mentioned that the contract size was 10mt (btw, I don't know what mt is, but let's just treat it as some standard unit) with the option delta being -0.2138 on 100 short call options. So, -0.2138 x 10 x 100 = 213.
For your put option question - in both cases, whether you're long or short the option the delta approaches 0 as the underlying price increases. Your long/short position just determines whether your delta will approach 0 from a positive number or a negative number. Also, the concept of ITM/OTM doesn't depend on your long/short position either. If a put has a strike price of 90 and the stock is expires at 100 then the put option is OTM. If you are long at the expiration date your position is worthless and you loss is the premium. If you are short the position is still worthless, however, you make a profit - being the premium received for selling the option.
Let me know if anything is unclear.
darrylApril 30th, 2012 at 4:37pm
Hi Peter,
I'm new to the greeks and wanted to pick up on the last comment. Why if delta is -0.2138, why would you buy 213 lots rather than 21?
In addition, 'I.e. for a long put if the underlying price increase from 50 to 60 the delta will go from -0.40 to -0.20 (longer)'. - i undertsand this as the option moves further otm and so delta moves closer to zero.
'For a short put the delta is reversed. So as the underlying price goes from 50 to 60 the short put delta will go from +0.40 to +0.20 (shorter)'. - If i'm short a put and the underlying price increases then doesn't my option move closer to/become more itm, so doesn't my delta increase?
Many thanks
PeterMarch 26th, 2012 at 8:58pm
Hi Charlie,
If the contract size is 10mt then your position delta, which is the amount that you need to hedge is 213 contracts (shares).
The value change to your position according to the delta isn't with "every" 1 point move - just with the first. Because, as you've indicated the delta itself will change as the underlying changes, which is given by the gamma.
So after the underlying has moved 1 point you will have a new delta and gamma value.
Also, gamma is basis a 1 point move unless it is specified as 1% gamma.
CharlieMarch 23rd, 2012 at 12:54am
Hello Peter, i have new software for options portfolio/prcing, and with a postion i have on the delta is -0.2138 (short a call) and the gamma -0.0158. If I am 100 lots short of the call (contract size = 10mt) then to be delta hedged i would need to buy 21 lots. As i understand correctly, the delta also means that the value of my position would decrease by $213 with every tick upwards. However in this instance the gamma of -0.0158 would mean that my delta goes shorter by -1.58 lots every % point higher NOT every tick higher (otherwsie gamma would be too big). The gamma value of the trade says -$15.8 which i think means the delta will decrease by this value for every % move upwards? Can you help. You agree confusing that delta is basis one tick move and gamma basis 1% move?
NaveFebruary 10th, 2012 at 12:53am
Great work Peter
PeterNovember 5th, 2011 at 4:06am
Hi Rick,
Yes, that's correct. Both calls and puts have the same gamma value, which will decrease either side of ATM.
RickNovember 4th, 2011 at 8:45am
Hi I want your feedback
If a call, initially otm, and then the stock price approaching the exercise price, the gamma would increase, when the call is in the money, gamma would decrease?
If a put, initially OTM, then if a stock price decreases, gamma would increase, and when the put is in the money, gamma would decrease if the stock still going down?
Am I saying the right things
THX
PeterJune 5th, 2011 at 5:55am
Hi Peter87, it might help to take a look at the delta graphs on the option delta page. Take a look at the Put Delta vs Underlying Price graph.
This represents a long put - so just reverse the numbers for a short put.
I.e. for a long put if the underlying price increase from 50 to 60 the delta will go from -0.40 to -0.20 (longer).
For a short put the delta is reversed. So as the underlying price goes from 50 to 60 the short put delta will go from +0.40 to +0.20 (shorter).
Peter87June 4th, 2011 at 8:06am
Thanks for your detailed and fast answer!
I got the part concerning calls and long puts but not the part with short puts: A short put has a concave (and negative) pay off profile. So, the higher the underlying value gets, the more approaches the pay off line the x-axis which implies that the slope (<=> delta) becomes bigger (= less negative = approaches 0).
That's why I don't get it that the position in a short put becomes shorter when the underlying price increases. In my opinion the position becomes LESS shorter (it becomes longer). But I guess there must be some reasoning errors in my argumentation!? :-)
PeterJune 4th, 2011 at 6:36am
The Delta depends on the option; call options have a position Delta and put options have a negative Delta. So, if you "sell" an option the call with have a negative Delta and the put a positive Delta.
Now, given that Gamma is positive for both calls and puts, if you sell an option your Gamma with therefore be negative.
When you're short an option and hence short Gamma both a short call and short put will "lose" Delta as the underlying price rises - this is also refered to as being "shorter".
For a call option, as the underlying price rises the option itself becomes more in-the-money and hence the Delta will move from 0 to 1. But if you are "short" the call the opposite happens meaning that the option Delta of your position will move from 0 to -1 (getting shorter).
For a put option, as the underlying price rises the option itself becomse more out-of-the-money and hence the Delta will move from -1 to 0 (getting longer). But if you are "short" the put the opposite happens meaing that the option Delta of your position will move from 1 to 0 (getting shorter).
Let me know if this is not clear.
Peter87June 3rd, 2011 at 2:47pm
I'm a beginner in options but understand almost the whole article. What I just don't understand is this:
"Conversely, if you sell options, and are therefore "short gamma", your position will become shorter as the underlying price increases [...]"
Delta (as first derivative) is negative and grows with increasing Underlying price, so it becomes LESS negative which means "less short" <=> "more long" !?!?!?!?
I would appreciate your feedback!
PeterNovember 3rd, 2010 at 4:54am
Are you talking about the video on this site above? That's where I say "take a look at this video". Then I provide a link to the OU site. The video above on "this" site does indeed do more than "describe" what gamma is and elaborates on gamma trading.
Please let me know if I have missed something or if you think the video above is incorrect.
trader1November 2nd, 2010 at 11:20pm
i clicked on the "options university" link under the long gamma trading heading,
it says you can see a video that gives an overview of gamma trading.
instead of a video that gives an over view of gamma, it is a 100 percent sales video for options university. NO GAMMA EVEN MENTIONED. rip off.
samJuly 28th, 2010 at 9:06pm
you are right. delta of put is decreasing function from -1 to 0 as the stock price increases. I was thinking in terms of absolute value of delta...
PeterJuly 28th, 2010 at 6:10pm
Hi Sam, it's a good question. You have to remember that a put's delta is negative so with a positive gamma and an increasing stock price the delta of a put becomes less negative - or "longer". The more the stock rallies the closer the put's delta approaches zero as more gamma is added to it.
Call options, with a positive delta and positive gamma will also "get longer" as the stock price rises. The higher the stock moves away from the strike price the closer the call option's delta approaches 1.
samJuly 28th, 2010 at 4:14pm
May be I am missing something. Mathematically, gamma is always positive for both call and put.
But as the stock price increases, shouldn't the put have negative gamma as the graph of put delta vs stock price is decreasing? Please someone clarify
Seth BakerFebruary 9th, 2010 at 3:04pm
This is interesting stuff. I use google to help me find stuff about options. One cool site has a different approach - they claim to not have an opinion on the market. Rather, they work with you on which type of trade to make, based on the Greeks, etc. I may spell this wrong, but I think it's http://www.timeforoptions.com
PeterOctober 8th, 2009 at 7:05pm
Hi Anthony, I agree that the video doesn't get off to a good start...I link directly to the video on the OU site. They've changed the video to what they've had previously, which provided a longer introduction.
At the start of the video Ron has already begun discussing "short gamma", where if you are short gamma and the market is going down your position gets "longer" i.e. your delta position grows. That's what he means when he says "buying deltas" on the way down.
Do you think my description (not the video) above differs from what you've read elsewhere? If so, let me know where the contradiction is and if I'm wrong I'll correct the content accordingly.
Thanks for the feedback!
AnthonyOctober 7th, 2009 at 10:39pm
I am learning to trade options by the greeks (delta, gamma, theta, vega) but have traded options for many years. I have looked up several definitions and am doing an online course. This definition here and the subsequent video are by far the most confusing I have ever come across. The video begins with "In a sense on the way down, our short gamma position is buying deltas for us...". How in the heck can someone trying to understand Gamma as a definition begin to understand this.
PeterSeptember 20th, 2009 at 8:09pm
Thanks for the suggestion...much appreciated. I'll write up something on delta neutral trading and a bit more on gamma scalping.
HowdySeptember 20th, 2009 at 10:38am
I have basic knowledge of options buying and selling calls and puts.
I would appreciate it if more detailed explanation is added in for gamma and delta trading. I am still confused as to how gamma trading works.
Thanks
Add a Comment