Vega Graphs - When is Vega Highest?
Like all other option Greeks, Vega isn't linear; it changes constantly as all other inputs to the pricing of options change. Some factors have a greater impact on the pricing of options than others. Below you'll find illustrations of the various affects these factors can have on the Vega values of options.
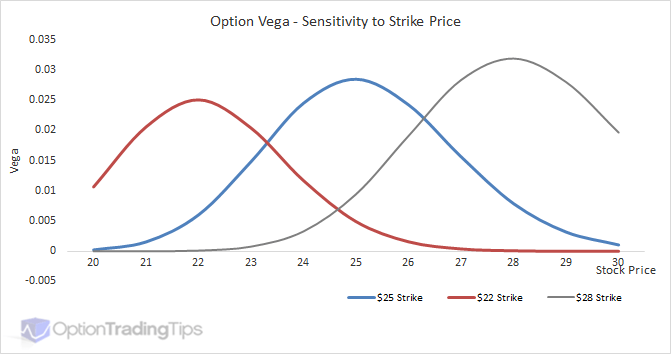
Vs Strike
ATM options are most sensitive to changes in volatility and therefore have the highest Vega values. Vega then tapers off towards OTM and ITM option strikes.
Vs Time
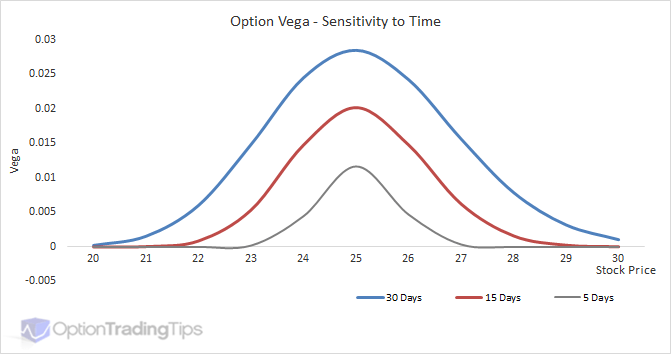
Volatility and time are basically the same thing when it comes to option valuation. Adding more volatility to an option is the equivalent of adding more time; that is, it increases the value of the option. The reason is that increasing either of these elements increases the likelihood of the option being in-the-money by the expiration date.
Vs Volatility
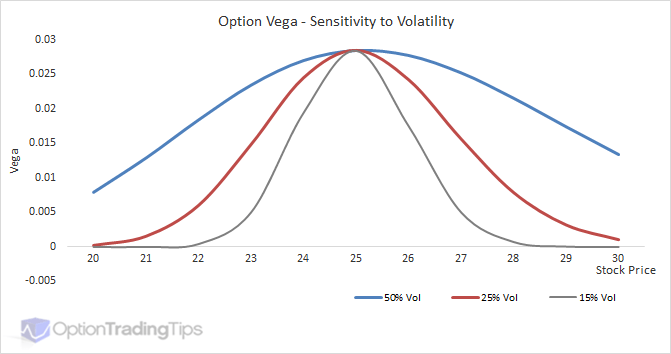
Long and Short Vega Positions
Vega has the same value for calls and puts and its' value is a positive number. That means when you buy an option, whether call or put, you have a positive Vega. This is also called being long Vega.
As Vega is effected by volatility, a long Vega position means you want the volatility to rise. When volatility rises, it will increase the value of the option by the Vega amount for every 1 % point move in the volatility. As you are long the option, the increase in the value means an increase in profit.
Conversely, short Vega positions expect volatility to fall in order to profit from a decline in option premiums.
Vega Option Chain
While theoretically the Vega is highest for ATM strikes, in practice this doesn't always happen. In the above Vega vs Strike graph, all other factors in the pricing of the option remain constant, except the strike price. I.e. The volatility input used for the pricing model is the same regardless of whether the option is ITM, ATM or OTM.
In reality, however, the implied volatility as determined by the market prices of the options are not constant; they vary across the strike range and form what's known as the Volatility Skew.
Because the volatility input is different, this can sometimes mean that the strike with the highest Vega isn't always smack on the ATM strike price. Take a look at this option chain of Amazon stock (AMZN).
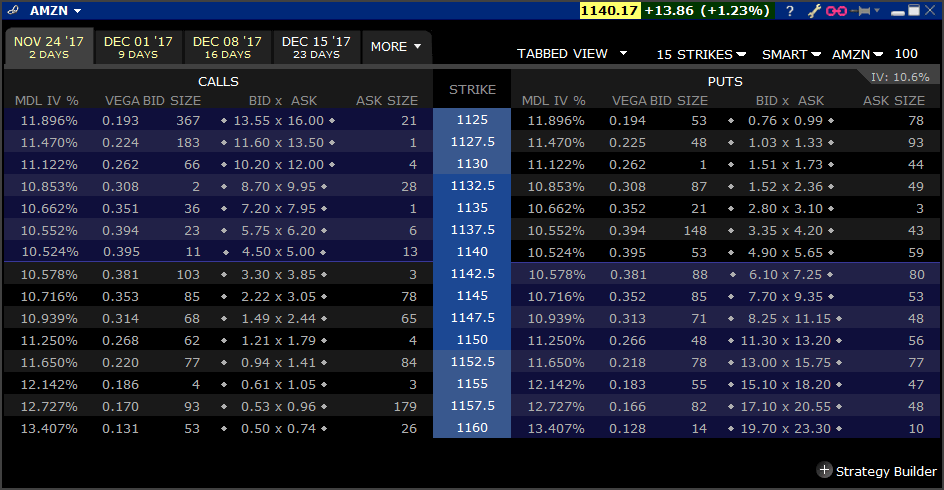
I chose AMZN as it is a high priced stock, which will mean higher Vega values to observe.
These options are only 10 days out, so the forward price for this expiration will be pretty close to the stock price, which is currently 1,140.17. At this stock price the ATM strike on screen will be 1140. The Vega for this strike is 0.395. In this case, the ATM strike does indeed have the highest Vega as the strikes either side taper off and decrease as you move away from the ATM price.
However, notice the implied volatilities shown in the "MDL IV%" column? The vols show the opposite curvature to the Vega; the ATM price is the lowest while the either side of the ATM strike the implied vols increase. The changes to the volatility with this expiration aren't large enough to change the Vega values in this case, but if you do notice higher Vega values outside of the ATM strike, this is likely why.
Black Scholes Vega
Check out my spreadsheet for a working example of Vega using Black and Scholes. Otherwise, here are some code examples:
Excel VBA
Option Vega Formula
Vega = 0.01 * UnderlyingPrice * Sqr(Time) * NdOne(UnderlyingPrice, ExercisePrice, Time, Interest, Volatility, Dividend)
Where:
NdOne = Exp(-(dOne(UnderlyingPrice, ExercisePrice, Time, Interest, Volatility, Dividend) ^ 2) / 2) / (Sqr(2 * 3.14159265358979))
dOne = (Log(UnderlyingPrice / ExercisePrice) + (Interest - Dividend + 0.5 * Volatility ^ 2) * Time) / (Volatility * (Sqr(Time)))




James ZhangSeptember 28th, 2017 at 8:56pm
Hi guys,
I have come across an estimation question regarding estimating the 1 day 99% VaR for various positions.
Say I'm shorting $1000 of one month vega, what would be my 99% VaR? what is a reasonable way to estimate?
Question 2:
And also if I'm shorting $1000 cash delta, in order to estimate 1 day VaR 99%, is it right to do this way?
Assume daily volatility of 1%, and assume normal return.
Then the VaR = 1% * Z(99%)*1000 = 1%*2.33*1000 = 23.3?
Question 3:
Is there a difference for estimating VaR between shorting and longing the same cash delta?
Many thanks.
PeterAugust 16th, 2017 at 12:13am
Hi Robert,
Yes, your table below is correct regarding the direction of the greeks based on the position you have.
RobertAugust 14th, 2017 at 9:21am
Hello, I have been delta neutral hedging (static) my underlying stocks. I made up this chart to help make decisions to balance out my positions; is it correct? I understand underlying stocks are Delta + but do not have Gamma/Vega....is this also correct? Thank you........
DELTA + DELTA -
LONG CALL SHORT CALL
SHORT PUT LONG PUT
LONG UNDERLYING SHORT UNDERLYING
GAMMA/VEGA + GAMMA/VEGA -
LONG CALL SHORT CALL
LONG PUT SHORT PUT
THETA + THETA -
SHORT CALL LONG CALL
SHORT PUT LONG PUT
PeterMay 30th, 2014 at 12:56am
Hi Josh, apoligies for the delay - this one slipped through the cracks.
To buy Vega or go long Vega means to be betting that volatility will increase irrespective of the direction of the asset.
josh zhangMay 12th, 2014 at 1:28am
hi all, sometimes forex strategists would recommend buy vega, or long vega, do you know what does that mean? many thanks, josh
PeterSeptember 30th, 2013 at 7:08pm
Ah yes, I had it back to front. October will lose from a rise in IV while December will benefit.
I understand what you're saying but the problem is that each position Vega won't move at the same rate. Because you're "total" Vega is made up of two individual Vega positions you need to take that into account because it is a spread. In your case, even though your total Vega was positive the front month had a large increase in IV that caused your position to lose money.
The problem is that Vega doesn't move in a linear fashion. The changes in Vega that result from a move in the underlying take the shape of a bell curve and not always easy to predict when you're combining option legs from different months.
Perhaps your TOS screen has a different risk value that you could use. Maybe a "Time Weighted Vega" column exists that you could use?
HarsonoSeptember 29th, 2013 at 9:57am
Dear Peter,
from your answer :" What you have is a spread where one leg benefits (OCtober) from a rise in IV where the other leg (December) loses from the rise in IV."
I think this is opposit of my posisition, my position is sell october ( Negative Vega )and buy December ( Positif Vega ).
I think if IV increase, I loss my short term Vega ( October ) and gain in my long term Vega ( December ). But my net Vega is positif ( it mean my long term Vega is bigger than my short term Vega ), so if IV increase, in this posisition, I will have some gain, but in my real account , it become loss, so I said before that the Vega works opposit from theory.
This loses, is not combine with gain from increase at underlying and gain from time decey yet, if I combine togather, it means the loss form Vega is huge percentage.
So until now, I still confused, how come Vega works seems reverse from theory.
Thank you.
PeterSeptember 29th, 2013 at 5:49am
Hi Harsono,
The IV is the same, yes, but your position (long/short) will determine the result when the IV moves.
If you are long volatility (long Vega) and the IV rises this will have a positive effect on your position. However, if you are short Vega and IV rises this will be negative for your position.
What you have is a spread where one leg benefits (OCtober) from a rise in IV where the other leg (December) loses from the rise in IV.
HarsonoSeptember 27th, 2013 at 11:47am
Hi Peter,
Thank you for your fast reply.
About the IV, I mean the IV is same for long or short contrack is like this :
said IV for GOOG at 20 September was 23.82%, The IV yesterday was 25.24. So this IV is cannot change , even we have long or short contrack.
Here , I copy the answer of my similar question, but honesly I still confuse about the thier answer :( from other web )
"with a calendar you are either buying or selling vega; when you buy a calendar, you are selling front month and buying back month, so you are selling vega, you expect vega to go down; you are selling vega to capture the higher premium, then buying vega back after it drops; here IV has increased so it has gone against you (so far) "
Peter, how do you think about this asnwer ? I think not right , is't it ?
Thank you.
PeterSeptember 26th, 2013 at 7:38pm
Hi Harsono,
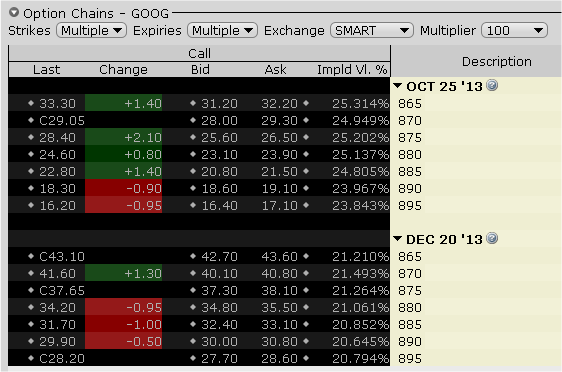
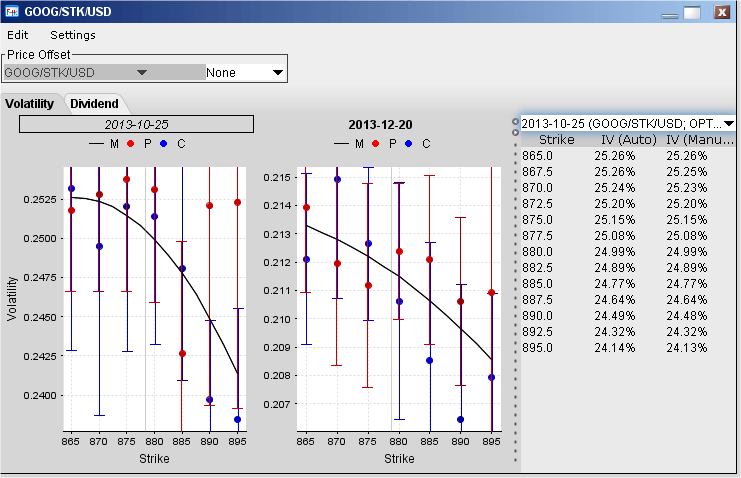
The IV won't be the same for all contracts and especially not for all maturities. Does your TOS show constant IV's across all option contracts? If so, this is not correct. This is a screen grab of Oct/Dec GOOG call options taken from my Interactive Broker's platform;
And here is a graph of the volatilities across strikes for both months;
Perhaps TOS just averages out the IV for all strikes and reports that number in your risk?
For your second question - it depends on your view of volatility. If you believe that the volatility is low and expect it to rise, then yes, buying options (long Vega) is a reasonable play. Even better is if the volatility is low before earnings rather than after.
harsonoSeptember 26th, 2013 at 5:23am
Dear Peter,
Thank you for your explanation, even I cannot get it clearly, it may cause by my English.
At your table, the Vega value is depand on contrack term, I agree with that, but at last colom, the IV , I think IV doent depend on contrack term.
The IV for long term contrack or short term contrack, is same. The IV for today, is same IV for all contrack, even long term or short them.
Peter, how about my second question : If we buy an option with positif vega ( big value of Vega ), it is better we buy at lower IV ( said few days after earnings ) ?
It it true of not ?
Thank you.
PeterSeptember 26th, 2013 at 12:28am
Hi Harsono,
OK - I've thought about it some more, done some simulating with my spreadsheet and think I have figured it out! Thanks for asking the question btw - it will serve as great value for other readers.
Hopefully I can explain it properly.
First, yes, your calculation of Vega is correct - (% Points x Vega x Contract Size). However, as you mentioned you are looking at the Vega of your spread position, which will be the October Vega less the December Vega.
But...the thing is, you are comparing this "spread" position Vega with the IV of the spread, which is likely the average of the two months IV. So, what I think has happened is that volatility has increased for both October and December, however, October has increased by more, which is why you have realised a loss. For example, let's say your original position looks like this;
So I guess the point is that when dealing with calendar spreads you have to be careful when looking at total spread IV when determining risk.
Does this make sense? Let me know if I've missed something or if you disagree.
harsonoSeptember 25th, 2013 at 1:34am
Dear Peter,
The value of Delta, Thetha and Vega, I meantion before is net Delta, Net Thetha and net Vega, because I bought CALENDER STRATEGIS ( Multy Legs )
I get these value ( Net Delta, Thetha and Vega ) From TOS ( Think or Swim ), a broker of America.
I also get The IV ( Impled Volatility ) also from TOS, my trading is real account.
I bought this option ( Underlying GOOG ) on 29 Augst, at that time IV was 23.81% and when I check again at 11 September , the IV become 24.28%.
Peter, I change my question become simple one, If I buy an option , price 6.55 with Vega positif, said 888 ( same meaning 0.888 ). If the IV increase from 25% to 27%, and the other factor are unchange, I will get gain 1.776 ( 2 x 0.888 ), it mean the price for this option become 8.326 ( 6.55+1.776 ) , this is right or not ?
In other words, if the Vega Posiftif , with big value, we should buy the option, when the IV is at lower lever ? This is right ?
Peter, so sorry if my english is not good, because English is not my mother tongue. Could you answer my 2 question above ? Because I trascation in option in big amount, but I am not sure about the VEGA.
For Others like Delta, Gamma, Thetha, Rho I can understand cleary, but Vega I am not sure,because I already try at my real account, but VEGA works opposite from the theory.
Thank you .
Rgds,
Harsono
PeterSeptember 23rd, 2013 at 8:14pm
Hi Harsono,
I see now. I think the confusion is likely to be related to the volatility. You've mentioned that the IV at the time was 23% - but where does this value come from? Is it a published number that you're using?
The reason I'm being specific here is that your spread is made up of two options that expire in different months - each will have a different volatility. Typically the back months have higher implied volatilities as the markets are less certain as time increases (expcept if the market is unusually volatility where traders might expect future volatility to come off current levels).
So it could just be that the back month option IV has dopped while the front month has risen netting out to be a decrease in overall IV for the spread.
Sorry I couldn't answer specifically - it's hard to answer without all the numbers, which I understand are difficult to come by at this point.
harsonoSeptember 19th, 2013 at 6:22am
Oh sorry Peter,
I forgot to tell you, I bought Calender Strategic, Sell October , Strike 910 and Buy Desember , Strike 910. Option price :6.8.
IV at that time was 23%
Delta = Positive 64, Theta positif 223 and Vega positif 831.
After Few day, the GOOG price increse , the IV also increase to 24.5%, but my option price down to 6.6 ( it mean I loss $20 per contrack ), how come be like this ?
The price of this posisition should have some gain ? Because the Delta is Positif, and the underlaying is increase , the Theta is positif, it means I should get some time decay value, and also the Vega is positif, The IV increse 1.5%, I should get some gain also.
But in actual trading , why my posisition of this underlying ( GOOG ) become loss ?
Thank you.
PeterSeptember 17th, 2013 at 4:42am
Hi Harsono,
Apoligies - I'm not exactly sure of your example - is this an outright option or an option spread? I ask because you've referenced two months. Also, the Theta for an outright long option will be negative.
So is the 6.8 price the total combo price or one of the legs?
harsonoSeptember 16th, 2013 at 10:52am
Dear Peter,
Thank you for your explanation .
But in actual trasaction, I buy GOOG , - October + November at stike 910 on 10 September, the underlaying at 888,1 the option price was 6.8. IV at that time was 0.23.
Delta = Positive 64, Theta positif 223 and Vega positif 831.
Today, the underlayingGOOG become 890.05 (increase ) IV now = 0.245 ( increase ), and of couse the I get some theta value, but now my option price become 6.6. Why ?
However, the option price should be more than 6.8 ?
Thank you.
Harsono
PeterSeptember 9th, 2013 at 5:48am
Hi Harsono,
A negative Vega means that the value of your long position will decrease if the volatility of your position increases.
I.e. say the position Vega of your spread is -0.65 and you paid 19.50 for the position. If the volatility increases from 30% to 31% then, all other things remaining unchanged, the value of your position will decrease to 18.85 (19.50 - 0.65).
harsonoSeptember 6th, 2013 at 10:44am
Dear Peter,
When I buy option with butterfly strategic, the net vega is negatif in huge number, what is mean ?
And I should buy at this strategic( butterfly ) , when the IV at low lever or high lever ?
Thank you.
PeterAugust 2nd, 2012 at 5:53am
Hi Vega,
I think the shape of the vega is consistent with the shape of volatility curve. The shape definitely shouldn't be linear as option prices do not follow a linear curve.
VegaAugust 1st, 2012 at 4:08pm
Hi,
I have the same question as someone ask as above. Whey is vega has a bell-curve shape. I assume the the vega should be different for in-the-money and out-of-money options?
Any insights?
PeterJanuary 26th, 2012 at 5:58pm
The symmetrical comment below was in reference to the fact that Vega is the same value for calls and puts.
I agree that the Vega values for OTM options will have a larger percentage increase on their prices than for ITM options, however, the absolute values for Vega does indeed taper off either side of ATM to shape a bell type curve.
enterJanuary 25th, 2012 at 7:48am
why is the vega symmetrical? wouldnt it make sense for the option price to be more sensitive to volatility when it is out of the money as opposed to in the money?
Considering, when the option is out of the money, the volatility increasing represents a higher chance of the option paying out money at the end of the day. When its in the money, the option is already most likely going to pay out money, so an increase in volatility cant (potentially) change the price as much.
PeterJuly 9th, 2011 at 7:06am
You mean symmetric for calls and puts? Then yes, as Vega is the same for calls and puts.
JohnJuly 8th, 2011 at 7:01am
Hi,
Thanks for this. Are the curves symmetric?
Cheers
PeterMay 2nd, 2011 at 8:39pm
Vega estimates how much an option will gain or lose in value as the volatility of the underlying asset changes.
It is useful to be able to measure the amount of risk your portfolio has in relation to swings in volatility.
shrutikaMay 2nd, 2011 at 2:38am
What is the Vega of an option and why is it useful? Discuss the steps you would undertake to make a portfolio Vega neutral?
PierreMarch 11th, 2011 at 12:18pm
So actually the value of the stock is fixed. Thanks Peter, I think I get it.
PeterMarch 9th, 2011 at 5:24pm
That's because Vega is the output generated from a pricing model, which is applied to an option. The option is "based" on an underlying, which can be a stock. The stock cannot have any vega because the stock "is" the underlying and doesn't have a strike price, expiration date etc.
You're probably looking at the standard deviation of the returns of a stock's movement and comparing this to the Vega of an option, which is not the same thing.
PierreMarch 9th, 2011 at 5:13am
Hi,
can anyone explain me why the vega of the underlying is 0? I have read it in the Hull but don't really understand where it comes from, since when I happen to differentiate the stock price -modelled e.g. by a geometric brownian motion- with respect to sigma, the quantity does not look like 0 to me!
Thanks in advance
PeterMarch 5th, 2011 at 9:59pm
Do you mean forecasting volatility? I've never come across any methods that use Vega to forecast volatility before. I've heard of methods such as GARCH that attempt this but I don't have any experience with these strategies so I can't comment directly.
ThrobMarch 5th, 2011 at 5:15pm
Can vega be used to "theorized" expected forward IV spots?
PeterJanuary 17th, 2011 at 5:25am
Hi Pankaj, Vega is always positive for calls and puts for both European and American options. This is because an increase in volatility always increases the theoretical value of an option - call or put.
PankajJanuary 16th, 2011 at 7:59pm
Hello friends,
Can anybody explain why Europeon Call option in Black-Scholes Model has always +ve Vega.
PeterDecember 30th, 2010 at 9:23pm
Hi Damola, check out the option greeks overview page first and let me know if you have any follow up questions.
damolaDecember 27th, 2010 at 2:56am
hi guys
This page has added to me tremendously on first sight....thumbs up!!!!!!
pls i need to know the relevance of theses greeks cuz i am just starting out in trading.....pls help with direction...tnx
PeterDecember 19th, 2010 at 9:31pm
Check out the information page on Option Greeks, which will explain why Option Greeks are useful.
madhuriDecember 18th, 2010 at 3:59am
dear friend,
I couldn't understand why we should know about theta& vega greeks!
Add a Comment